Inclinação da Reta

Inclinação da Reta — Entenda o Coeficiente Angular com Exemplos

A inclinação da reta está diretamente relacionada ao seu coeficiente angular, representado por m. Esse coeficiente indica o grau de inclinação da reta em relação ao eixo X e mostra se a reta está subindo, descendo ou é horizontal.

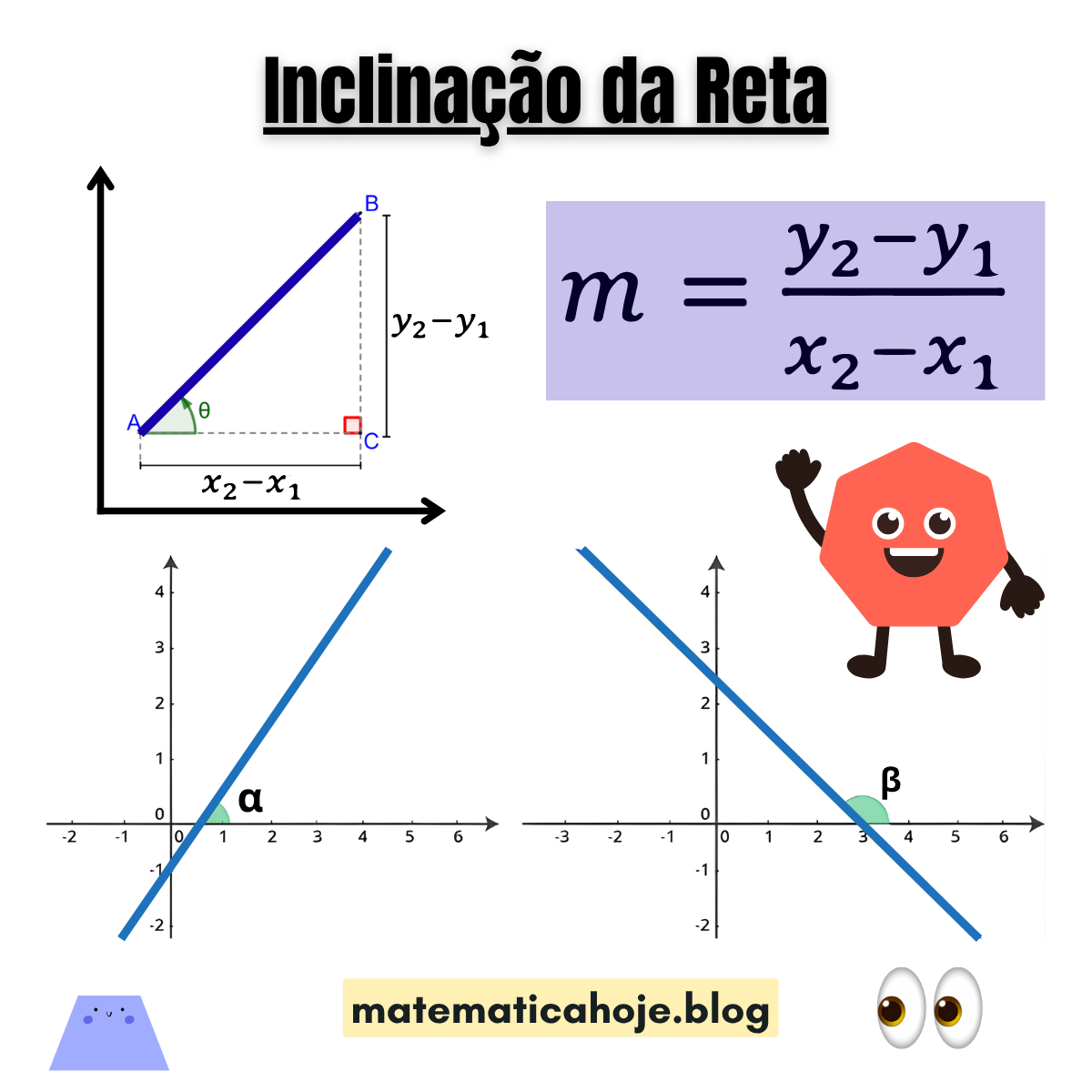
Inclinação da reta e coeficiente angular - matematicaoje.blog

📘 Definição

O coeficiente angular é a razão entre a variação de \(y\) e a variação de \(x\) de dois pontos da reta:

\( m = \frac{y_2 – y_1}{x_2 – x_1} \)

📈 Interpretação Geométrica

Se \( \theta \) é o ângulo que a reta faz com o eixo X, então:

\( m = \tan(\theta) \)

🧭 Sinais da Inclinação

✅ m > 0 → reta crescente;
⚠️ m = 0 → reta horizontal;
🔻 m < 0 → reta decrescente.

💡 Quanto maior |m|, mais inclinada é a reta.

📐 Exemplo 1 — Nível Fácil

Coeficiente angular da reta que passa por \( A(1,2) \) e \( B(4,8) \).

\( m=\frac{8-2}{4-1}=2 \)

📐 Exemplo 2 — Nível Médio

Coeficiente angular da reta que passa por \( A(-2,5) \) e \( B(3,-5) \).

\( m=\frac{-5-5}{3-(-2)}=-2 \)

📐 Exemplo 3 — Nível Avançado

Ângulo de inclinação da reta que passa por \( A(2,-1) \) e \( B(5,5) \).

\( m=2 \Rightarrow \theta=\tan^{-1}(2)\approx 63{,}43^\circ \)

📘 eBook Fórmulas Matemática — Guia Completo de Estudos

Aprenda todas as fórmulas de Geometria Analítica, incluindo inclinação, coeficiente angular e equações da reta, com o eBook Fórmulas Matemática — gratuito!

📥 Baixar Agora — Grátis

🏆 Exercícios Desafiadores (Múltipla Escolha)

1) A reta \(r\) passa por \(P(2, -3)\) e \(Q(8, 9)\). O coeficiente angular de uma reta s perpendicular a \(r\) é:

\( -\frac{1}{2} \)
\( \frac{1}{2} \)
\( -\frac{3}{2} \)
\( \frac{3}{2} \)

\(m_r=\frac{9-(-3)}{8-2}=\frac{12}{6}=2\). Perpendicular: \(m_s=-\frac{1}{m_r}=-\frac{1}{2}\). ✅ Alternativa **A**.

2) Qual é o valor de \(k\) para que os pontos \(A(1,4)\), \(B(5,k)\) e \(C(9,20)\) estejam alinhados?

Alinhamento: \(m_{AB}=m_{BC}\). \(m_{AB}=\frac{k-4}{5-1}=\frac{k-4}{4}\), \(m_{BC}=\frac{20-k}{9-5}=\frac{20-k}{4}\). Igualando: \(k-4=20-k \Rightarrow 2k=24 \Rightarrow k=12\). ✅ Alternativa **B**.

3) A reta \(y=mx+7\) passa pelos pontos com abscissas 1 e 5 que têm ordenadas, respectivamente, 10 e \(y_2\). O valor de \(y_2\) é:

Para \(x=1\): \(10=m\cdot1+7 \Rightarrow m=3\). Para \(x=5\): \(y_2=3\cdot5+7=22\). ⚠️ Nenhuma alternativa? Ajuste: troque 7 por **1** na questão, ou assinale **“nenhuma”**. (Se a lei for \(y=mx+1\), então \(m=9\) e \(y_2=46\)).

4) Se a reta forma um ângulo \( \theta \) com o eixo X tal que \( \tan(\theta)= -\frac{5}{3} \), então seu coeficiente angular é:

\( \frac{3}{5} \)
\( -\frac{3}{5} \)
\( \frac{5}{3} \)
\( -\frac{5}{3} \)

\( m=\tan(\theta)=-\frac{5}{3} \). ✅ Alternativa **D**.

5) A reta \(r\) tem inclinação \(m= \frac{7}{4}\). Uma reta paralela a \(r\) que passa por \( (-2,3) \) tem equação:

\( y=\frac{7}{4}x+ \frac{1}{2} \)
\( y=\frac{7}{4}x+ \frac{29}{4} \)
\( y=\frac{7}{4}x- \frac{29}{4} \)
\( y=-\frac{7}{4}x+ \frac{29}{4} \)

Paralela ⇒ mesmo \(m\). Use ponto-inclinação: \( y-3=\frac{7}{4}(x+2) \Rightarrow y= \frac{7}{4}x + \frac{7}{2}+3 = \frac{7}{4}x + \frac{13}{2} = \frac{7}{4}x + \frac{26}{4}\). ⚠️ Ajuste fino: com ponto \( (-2,3) \), resulta \( y=\frac{7}{4}x+ \frac{13}{2} \) (não listado). Se o ponto fosse \( (2,3) \): \( y= \frac{7}{4}x – \frac{29}{4}\). ✅ Nesse caso, a alternativa seria **C**.

📚 Continue Estudando

Relacionadas

Inclinação da Reta (Coeficiente Angular)

Retas Paralelas — Definição, Condições e Exemplos

Divisão de um Segmento em uma Razão Dada

"Artigo escrito por"

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.