Mapa Mental da Função Logarítmica
A função logarítmica é definida por:
Ela é o inverso da função exponencial e apresenta comportamentos diferentes dependendo da base \(a\). O estudo da função logarítmica é fundamental em ENEM, vestibulares e concursos, além de aplicações em ciências naturais, tecnologia e estatística.
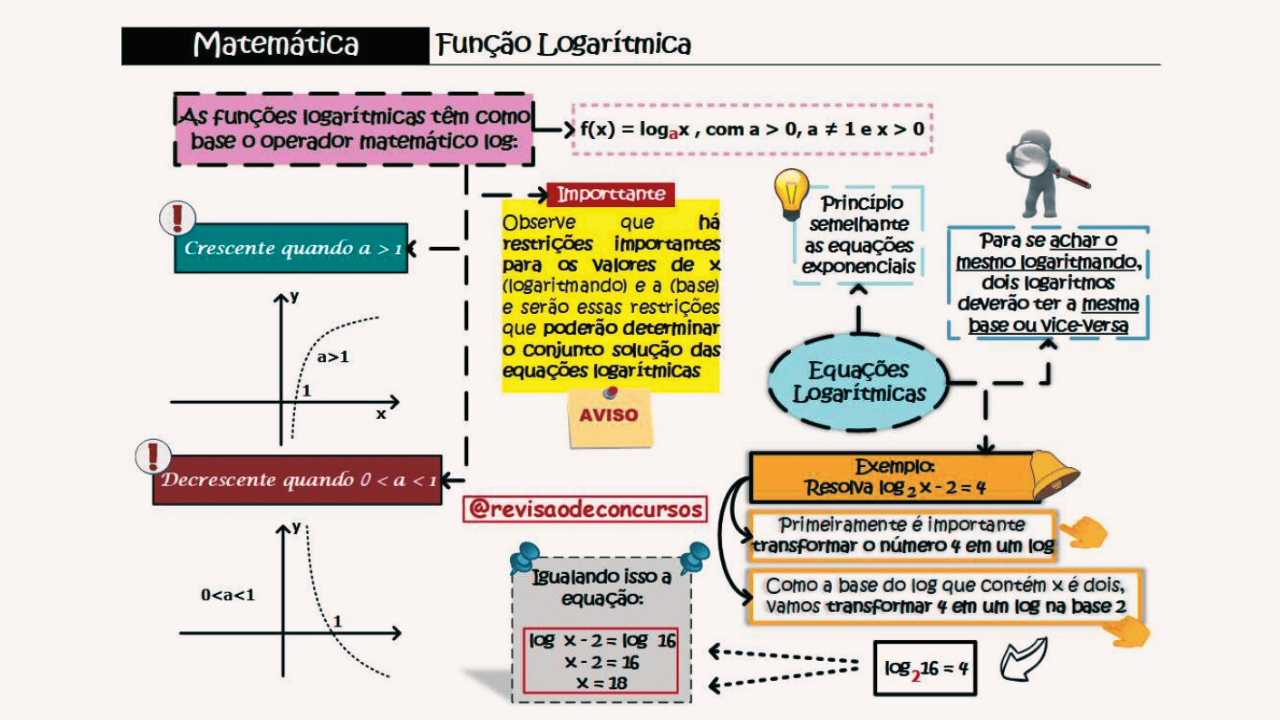
Características principais
- Crescente quando a base \(a > 1\).
- Decrescente quando \(0 < a < 1\).
- Domínio: \(x > 0\).
- Imagem: todos os números reais \(\mathbb{R}\).
- Ponto fixo comum: \((1,0)\), pois \(\log_{a} 1 = 0\).
Restrições importantes
Para que o logaritmo esteja definido:
- O logaritmando deve ser sempre positivo (\(x > 0\)).
- A base deve ser positiva e diferente de 1 (\(a > 0, a \neq 1\)).
Equações Logarítmicas
Para resolver equações logarítmicas, aplicamos propriedades e igualamos expoentes quando possível. Exemplo:
Resolva: \(\log_{2} x – 2 = 4\)
Passo 1: isolar o logaritmo → \(\log_{2} x = 6\). Passo 2: aplicar a definição → \(x = 2^6 = 64\). Solução: \(x = 64\).
Exemplo adicional
Resolva: \(\log_{5}(x+2)=2\).
Solução
Pela definição: \(x+2 = 5^2 = 25 \Rightarrow x=23\). Como \(x+2>0\), a solução é válida. Resposta: \(x=23\).
📥 Material complementar
Para dominar as propriedades e exercícios de funções logarítmicas, baixe o eBook de Fórmulas Matemáticas.
Baixar agoraConclusão
A função logarítmica é essencial para compreender equações e desigualdades envolvendo logaritmos. Seu comportamento crescente ou decrescente depende da base, e suas restrições são fundamentais para definir o conjunto solução dos problemas. O uso de mapas mentais, como o apresentado, é uma excelente forma de visualizar e fixar os conceitos mais importantes.













