Pirâmide regular

Pirâmide regular: definição, elementos, fórmulas, planificação e exercícios

Pirâmide regular

Definição, elementos, relações, fórmulas de área e volume, planificação e exemplos com contas na vertical.

Na pirâmide regular: base é um polígono regular; o vértice está sobre o centro da base.

1) O que é uma pirâmide regular?

Pirâmide é o poliedro com um polígono na base e faces laterais triangulares que se encontram em um vértice.
É regular quando a base é um polígono regular e o vértice está alinhado ao centro da base.

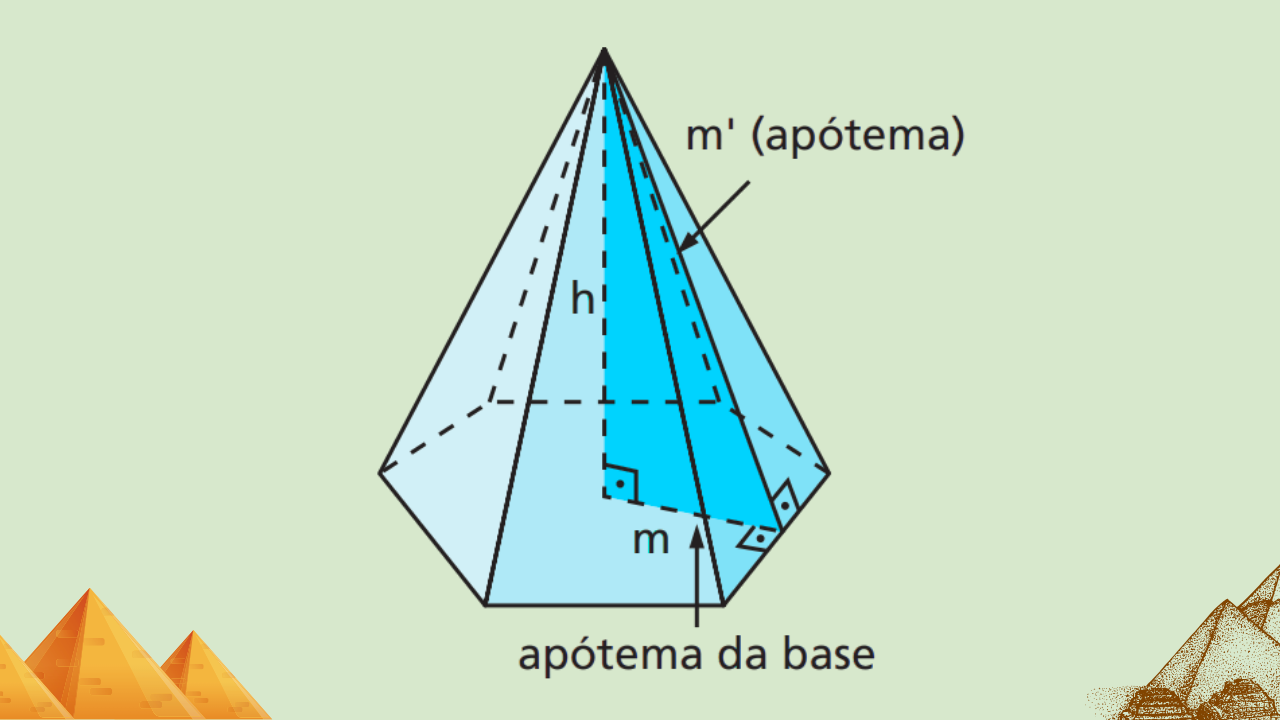
Elementos: $n$ (lados da base), $a$ (lado), $p=n\,a$ (perímetro), $m$ (apótema da base), $h$ (altura), $m’ \equiv g$ (apótema lateral), $l$ (aresta lateral) e $R$ (raio circunscrito da base).

2) Relações geométricas fundamentais

$(m’)^2 = h^2 + m^2 \;\Rightarrow\; m’=\sqrt{h^2+m^2},\; h=\sqrt{(m’)^2-m^2}$

$l^2 = (m’)^2 + \left(\dfrac{a}{2}\right)^2$ (na face lateral)

$l^2 = h^2 + R^2$ (plano vértice–centro–vértice da base)

Para base regular de $n$ lados, com $\theta=\dfrac{\pi}{n}$:

$m=\dfrac{a}{2}\cot\theta$, $R=\dfrac{a}{2\sin\theta}$, $p=n\,a$

Equivalências: $a=2m\tan\theta=2R\sin\theta$ e $m=R\cos\theta$.

3) Áreas e volume

Área lateral: $A_L=\dfrac{p\,m’}{2}$

Área total: $A_T=A_L+A_b$

Volume: $V=\dfrac{A_b\,h}{3}$

Bases regulares frequentes

Quadrada: $A_b=a^2$.
Triangular equilátera: $A_b=\dfrac{\sqrt3}{4}a^2$.
Pentagonal regular: $A_b=\dfrac{5ar}{2}$ (com $r=m$, apótema da base).
Hexagonal regular: $A_b=\dfrac{3\sqrt3}{2}a^2$.

4) Planificação

Formada por 1 polígono regular (a base) + $n$ triângulos isósceles de base $a$ e altura $m’$. A soma das áreas da base e dos triângulos é a área total $A_T$.

Compare com: Planificação do prisma pentagonal e do prisma hexagonal.

5) Guia rápido de resolução

Identifique a base: obtenha $a$, $n$ → calcule $p$, $m$ e $A_b$.
Se for área lateral/total, encontre $m’$ (direto ou via $m’=\sqrt{h^2+m^2}$).
Se for volume, garanta a altura $h$ (não confundir com $m’$).
Se for dada aresta lateral $l$, use $l^2=(m’)^2+(a/2)^2$ ou $l^2=h^2+R^2$.
Conferir unidades: $1\,\text{L}=1000\,\text{cm}^3$.

6) Exemplos resolvidos (contas na vertical)

Exemplo 1 — Volume (base quadrada)

Enunciado. Pirâmide regular de base quadrada com $a=10\,\text{cm}$ e $h=18\,\text{cm}$. Calcule o volume.

Ver solução

$$\begin{aligned} A_b &= a^2\\ &= 10^2\\ &= 100\ \text{cm}^2\\[6pt] V &= \frac{A_b\cdot h}{3}\\ &= \frac{100\cdot 18}{3}\\ &= \frac{1800}{3}\\ &= \boxed{600\ \text{cm}^3} \end{aligned}$$

Exemplo 2 — Área total (base equilátera)

Enunciado. Base triangular equilátera com $a=12\,\text{cm}$ e apótema lateral $m’=15\,\text{cm}$. Calcule a área total.

Ver solução

$$\begin{aligned} p &= 3a\\ &= 36\\[4pt] A_L &= \frac{p\,m’}{2}\\ &= \frac{36\cdot 15}{2}\\ &= 270\ \text{cm}^2\\[6pt] A_b &= \frac{\sqrt3}{4}a^2\\ &= \frac{\sqrt3}{4}\cdot 144\\ &= 36\sqrt3\ \text{cm}^2\\[6pt] A_T &= A_L + A_b\\ &= 270 + 36\sqrt3\\ &\approx \boxed{332{,}35\ \text{cm}^2} \end{aligned}$$

Exemplo 3 — Encontrar a altura a partir de $m’$ (base quadrada)

Enunciado. Em uma pirâmide regular de base quadrada, $a=8\,\text{cm}$ e $m’=13\,\text{cm}$. Calcule a altura $h$.

Ver solução

$$\begin{aligned} m &= \frac{a}{2}\\ &= \frac{8}{2}\\ &= 4\ \text{cm}\\[4pt] h &= \sqrt{(m’)^2 – m^2}\\ &= \sqrt{13^2 – 4^2}\\ &= \sqrt{169 – 16}\\ &= \sqrt{153}\\ &\approx \boxed{12{,}37\ \text{cm}} \end{aligned}$$

7) Exercícios propostos

Pirâmide quadrada: $a=6\ \text{cm}$, $h=10\ \text{cm}$. Calcule o volume.
Pirâmide equilátera: $a=8\ \text{cm}$, $m’=9\ \text{cm}$. Calcule a área lateral.
Pirâmide pentagonal regular: $a=5\ \text{cm}$, apótema da base $r=3{,}4\ \text{cm}$, $h=12\ \text{cm}$. Calcule o volume.
Pirâmide quadrada: $a=7\ \text{cm}$, $m’=11\ \text{cm}$. Calcule a área total.
Pirâmide hexagonal regular: $a=4\ \text{cm}$, $h=9\ \text{cm}$. Calcule o volume (aprox.).

8) Ligações internas úteis

Poliedros Fórmula de Euler Sólidos de Platão Prismas regulares Prisma pentagonal Prisma hexagonal Planificação — prisma pentagonal Planificação — prisma hexagonal Área de triângulo Triângulos semelhantes

9) Materiais do blog

🧠 Mapas Mentais de Matemática 🎯 ENEM Matemática 📚 Coleção 10 eBooks 🗃️ Banco de Questões de Matemática 📺 Canais Oficiais de Matemática

Relacionadas

Cubo: Definições, fórmulas e exercícios

Planificação do Prisma Triangular

Tetraedro Regular

"Artigo escrito por"

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.