Zeros ou Raiz de uma Função Quadrática

Zeros (raízes) de uma Função Quadrática: Bhaskara, gráfico e exercícios

Zeros (raízes) de uma Função Quadrática

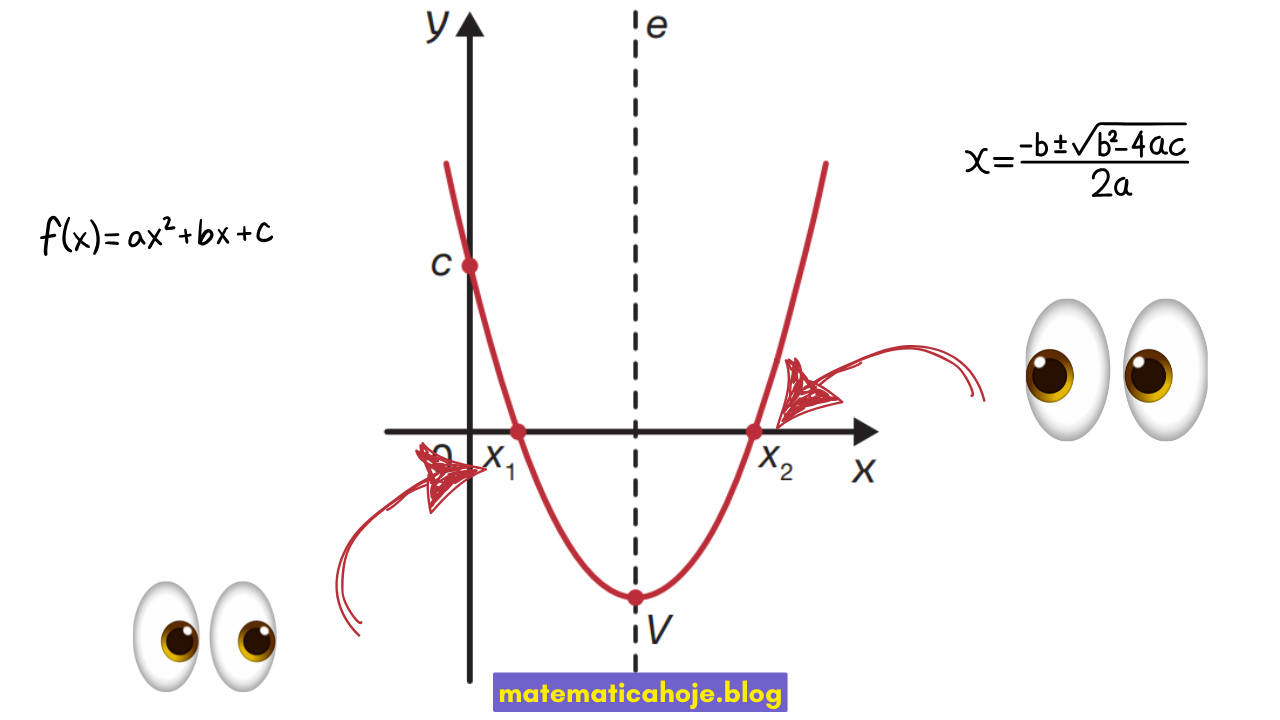
Os zeros (ou raízes) de \(f(x)=ax^2+bx+c\) são os valores de \(x\) que tornam \(f(x)=0\). Geometricamente, são os pontos onde a parábola corta o eixo \(x\). Eles se relacionam diretamente com o vértice, com o valor máximo/mínimo e com os coeficientes \(b\) e \(c\). Para ver a influência do sinal e do módulo de \(a\), confira o papel do coeficiente \(a\).

Ilustração com f(x)=ax²+bx+c e a fórmula de Bhaskara para encontrar as raízes da função quadrática.

Fórmula de Bhaskara e discriminante

\[ x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\quad\text{com}\quad \Delta=b^2-4ac. \]

\(\Delta>0\): duas raízes reais distintas (dois cortes no eixo).
\(\Delta=0\): raiz dupla (a parábola tangencia o eixo).
\(\Delta<0\): não há raízes reais (cortes só no plano complexo).

Relações úteis (Viète)

\[ r_1+r_2=-\frac{b}{a},\qquad r_1\cdot r_2=\frac{c}{a}. \]

Essas relações explicam como \(b\) e \(c\) controlam a soma e o produto das raízes.

Passo a passo para achar as raízes

Identifique \(a\), \(b\) e \(c\) em \(ax^2+bx+c=0\) (\(a\neq 0\)).
Calcule \(\Delta=b^2-4ac\).
Substitua em \(x=\dfrac{-b\pm\sqrt{\Delta}}{2a}\).
Cheque o gráfico para interpretar (veja o guia do gráfico).

📘 E-book de Fórmulas de Matemática

Bhaskara, forma canônica, vértice, discriminante e muito mais em um PDF enxuto para revisão rápida.

Quero o E-book de Fórmulas

Exemplos resolvidos (com contas em coluna)

Exemplo 1 — Duas raízes reais

Resolva \(x^2-5x+6=0\).

\[ \begin{aligned} a&=1,\ b=-5,\ c=6\\[2pt] \Delta&=(-5)^2-4(1)(6)\\ &=25-24\\ &=1\\[6pt] x&=\frac{-(-5)\pm\sqrt{1}}{2\cdot 1}\\ &=\frac{5\pm 1}{2}\\[6pt] x_1&=\frac{6}{2}=3,\qquad x_2=\frac{4}{2}=2 \end{aligned} \]

Exemplo 2 — Raiz dupla

Resolva \(x^2-6x+9=0\).

\[ \begin{aligned} a&=1,\ b=-6,\ c=9\\ \Delta&=(-6)^2-4(1)(9)\\ &=36-36\\ &=0\\[6pt] x&=\frac{-(-6)\pm 0}{2\cdot 1}\\ &=\frac{6}{2}=3 \end{aligned} \]

A parábola toca o eixo em \(x=3\). O vértice está sobre o eixo \(x\).

Exemplo 3 — Sem raízes reais

Resolva \(2x^2+x+2=0\).

\[ \begin{aligned} a&=2,\ b=1,\ c=2\\ \Delta&=1^2-4(2)(2)\\ &=1-16\\ &=-15\ (<0) \end{aligned} \]

Não há soluções reais; o gráfico não corta o eixo \(x\). Para a abertura e posição da parábola, veja o coeficiente \(a\).

Exemplo 4 — Usando Viète

Sabendo que \(f(x)=x^2-7x+10\), encontre as raízes sem Bhaskara.

\[ \begin{aligned} r_1+r_2&=-\frac{b}{a}=7,\quad r_1r_2=\frac{c}{a}=10\\ &\text{Pares que multiplicam 10 e somam 7: }(2,5)\\ &\Rightarrow r_1=2,\ r_2=5. \end{aligned} \]

Sinal de \(f(x)\) e ligação com máximos/mínimos

Com as raízes em mãos, é fácil estudar o sinal da função (intervalos onde \(f(x)>0\) ou \(f(x)<0\)), o que se conecta ao ponto de máximo/mínimo e aos pontos notáveis. Para uma visão geométrica completa (foco e diretriz), veja A parábola.

Exercícios propostos

1) Determine as raízes de \(3x^2-13x+14=0\).

Mostrar gabarito

\[ \begin{aligned} a&=3,\ b=-13,\ c=14\\ \Delta&=(-13)^2-4(3)(14)\\ &=169-168\\ &=1\\[6pt] x&=\frac{-(-13)\pm\sqrt{1}}{2\cdot 3}\\ &=\frac{13\pm 1}{6}\\ x_1&=\frac{14}{6}=\frac{7}{3},\quad x_2=\frac{12}{6}=2 \end{aligned} \]

2) Para \(f(x)=-2x^2+8x-6\), encontre as raízes e o intervalo onde \(f(x)\ge 0\).

Mostrar gabarito

\[ \begin{aligned} a&=-2,\ b=8,\ c=-6\\ \Delta&=8^2-4(-2)(-6)\\ &=64-48\\ &=16\\[6pt] x&=\frac{-8\pm\sqrt{16}}{2(-2)}\\ &=\frac{-8\pm 4}{-4}\\[6pt] x_1&=\frac{-8+4}{-4}=1,\quad x_2=\frac{-8-4}{-4}=3 \end{aligned} \]

Como \(a<0\), a parábola é “para baixo” e \(f(x)\ge 0\) para \(x\in[1,3]\).

3) Mostre que \(x^2+4x+8=0\) não tem raízes reais e dê as complexas.

Mostrar gabarito

\[ \begin{aligned} \Delta&=4^2-4(1)(8)=16-32=-16\\ x&=\frac{-4\pm\sqrt{-16}}{2}\\ &=\frac{-4\pm 4i}{2}\\ &= -2\pm 2i \end{aligned} \]

Continue o estudo (links internos)

Função Quadrática (guia completo) Gráfico da função quadrática Vértice da parábola Valor máximo e mínimo Coeficientes \(b\) e \(c\) Coeficiente \(a\) Pontos notáveis da parábola A parábola

Materiais recomendados (produtos do blog)

Mapas Mentais de Matemática Preparação ENEM Matemática Coleção com 10 E-books Banco de Questões de Matemática E-book de Fórmulas (referência rápida)

Relacionadas

Valor máximo e mínimo de uma função quadrática

Vértice da parábola

Forma fatorada da Função Quadrática

"Artigo escrito por"

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.